[자료구조]1.2 Primitive Type: Integer (1) 음수 표현

Intro

Integer(정수)에 대한 설명은 지난 포스트에서 간단히 다루었습니다.
[자료구조]1.1 Introductions to Data Structure 참고

이번 포스팅에서는 위의 포스팅에서 언급한 '범위' 를 기준으로 정수형을 나누기 전,
컴퓨터에서 정수를 나타내는 방법에 대해 설명하고자 합니다.

컴퓨터는 모든 명령어와 숫자를 2진법(binary)으로 나타냅니다.
정수(수학기호: ℚ)는 자연수(수학기호: ℕ)와 ‘0’, 음수를 포함합니다.
자연수와 ‘0’는 쉽게 2진법으로 나타낼 수 있습니다.
(e.g 0(ten) = 0(two), 13(ten) = 1101(two))

그렇다면, 음수는 어떻게 나타낼까요?
일반적인 방법은 signed-magnitude(부호화 절대값)방식입니다.
이진법으로 나타내되, MSB(the Most Significant Bit) 최상위 부호 비트로 부호를 구분합니다.
최상위 비트가 ‘0’일 경우는 자연수를, ‘1’일 경우는 음수를 뜻합니다.
(e.g 18(ten)=010010(two), -18(ten)=110010(two))

하지만, 이 방법에는 문제가 있습니다.
이번 포스팅에서는 컴퓨터에서 음수 표현 문제를 어떻게 해결하였는지
중점적으로 살펴보겠습니다.

Description

앞서 Intro에서 설명한 바와 같이, 정수 표현에서 문제가 되는 것은 음수 표현입니다.
MSB(최상위 부호 비트)를 사용할 때에 문제가 되는 경우는
서로 다른 부호끼리 더할 때 발생합니다.

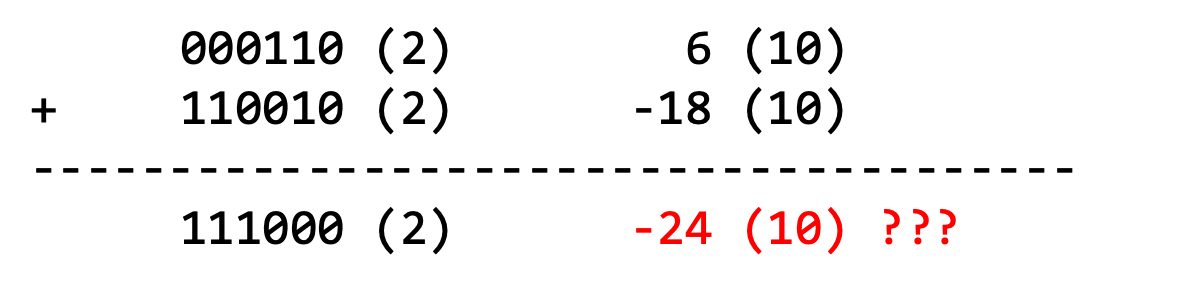
이와 같은 문제를 해결하기 위해 1’s complement (1의 보수) 방법이 등장합니다.

1’s complement

1’s complement(1의 보수) 방법이란? ()
음수에 한하여 모든 bit를 0 → 1 , 1 → 0 으로 바꾸어 계산하는 방법입니다.
단, MSB(최상위 부호 비트) 는 1로 유지 됩니다. -1은 다음과 같이 표현됩니다.

앞서 문제가 되었던 6 + (-18)의 계산 과정을 보겠습니다.

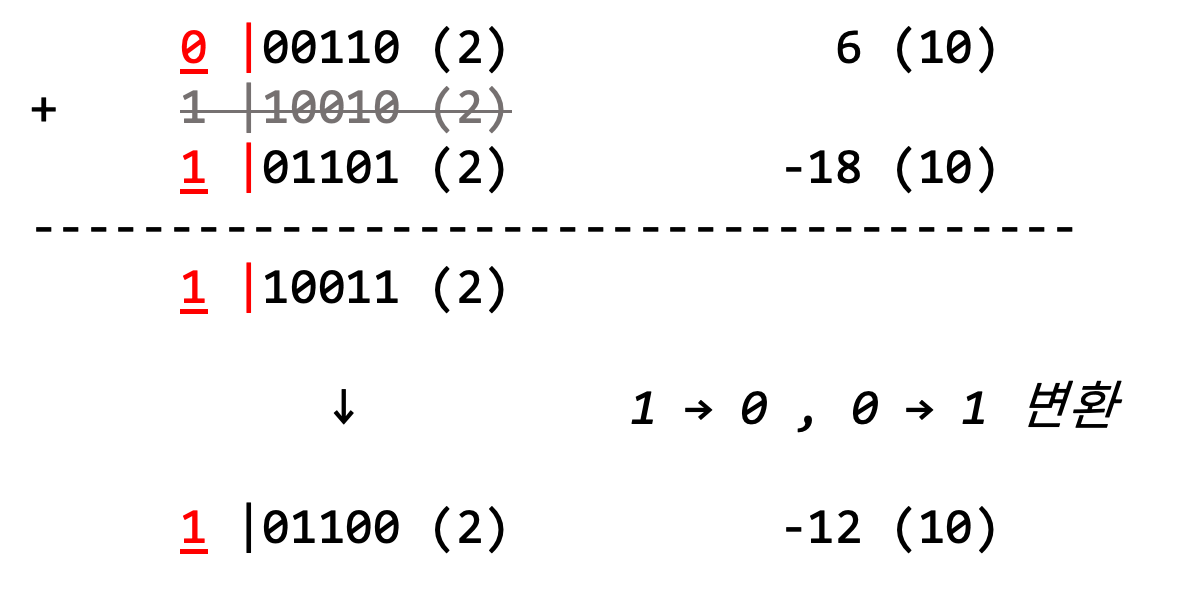
의도한 대로 답이 잘 나옵니다! 😃

그런데, 이런 경우에는 어떻게 할까요?

• 양수 + 음수 (단, 양수 > 음수)
  (1) 10 + (-2) = ?

• 음수 + 음수
  (2) (-10) + (-5) = ?

지정된 자리 이상으로 자리 올림이 발생할 경우, 1의 보수 방법에서는 carry bit을 사용하여
자리 올림이 발생할 때에 2진수의 맨 마지막 자리 bit에 1을 더하게 됩니다.

(1),(2)의 1's complement 방법의 연산과정 [클릭]

(1)의 경우

(2)의 경우

역시 원하는 대로 답이 나오게 됩니다. 😄

하지만, 1의 보수 방식에도 문제가 있습니다.
0을 표현하는 방법이 2개로 나뉘어 있기 때문이지요.

이를 보완 하기 위해 2’s complement (2의 보수) 방법이 등장하게 됩니다.

2’s complement

2’s complement(2의 보수) 방법이란?
1’s complement(1의 보수)와 동일하되, 연산 결과가 MSB가 음수를 나타낼 경우
2진수의 맨 마지막 자리 bit에 1을 더하는 방법입니다. -1은 다음과 같이 표현됩니다.

1의 보수 표현법에서 문제가 되었던 0을 표현하는 방법도
00000000(8-bit 기준) 으로 통일되며 해결됩니다.

일반적인 컴퓨터 프로그래밍에서는 MSB(최상위 부호 비트)를 확인하여 음수일 경우,
2’s complement(2의보수)방식을 사용합니다.
하지만 이 경우에도 문제가 발생할 수 있습니다.

바로 overflow 문제입니다.

overflow

overflow는 컴퓨터 프로그래밍에서는 정의한 범위를 벗어나는 경우를 뜻합니다.
2진수의 bit는 비트 갯수에 비례하여 10진수를 표현할 수 있습니다.

2진수의 bit 갯수를 n이라 하고,
기본적으로 0을 제외하고 표현할 수 있는 숫자 갯수(N)는 다음과 같습니다.

[4bit 기준 표현할 수 있는 숫자]

표 펼쳐보기

- unsigned 표현법 기준

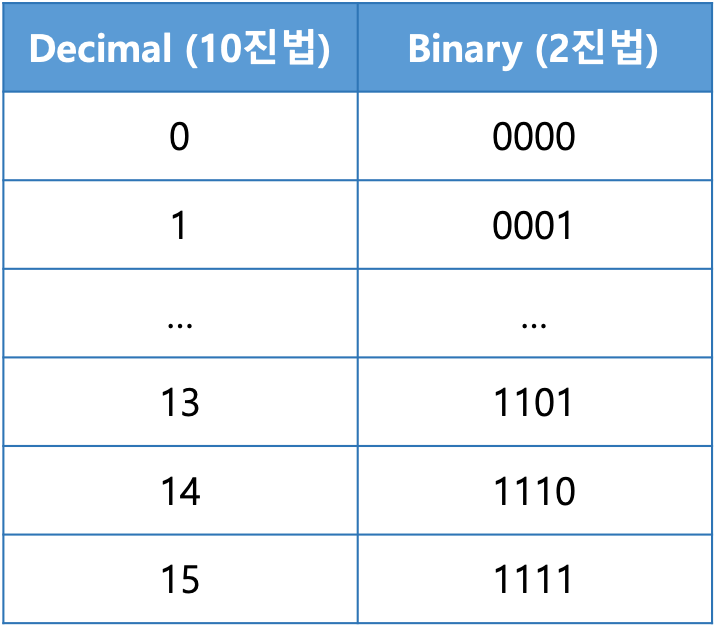
단, MSB(최상위 부호 비트)를 사용할 경우는 다음과 같습니다.
- 1's complement 표현법 기준

- 2's complement 표현법 기준

이 때, 같은 부호끼리 더하거나 곱할 경우 overflow가 발생하게 됩니다.

overflow를 처리하지 않을 경우 엉뚱한 결과 값이 나올 수 있으므로,
overflow가 일어났는지를 check할 bit가 추가적으로 필요하게 됩니다.
check 방법은 논리연산인 XOR을 사용합니다.
이 때, 두 피연산자의 결과가 XOR 결과 값과 다를 때,
overflow가 일어났음을 감지할 수 있게 됩니다.
A ⊕ B = ? 1 = true , 0 = false
[XOR 연산 결과]

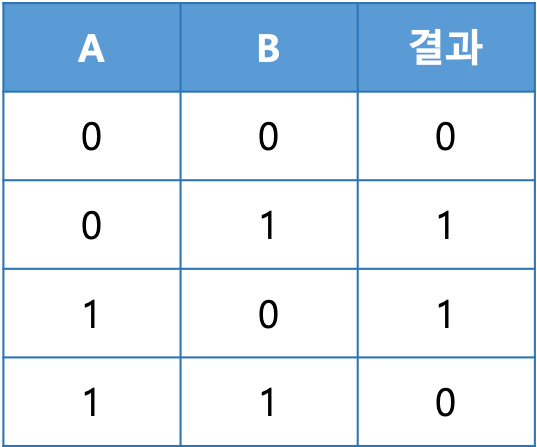
이로써 overflow를 감지하는 방법까지 알아보았습니다.
overflow를 처리하는 방법은 추가 포스팅에서 더욱 자세히 설명하도록 하겠습니다.

Summary

이번 포스팅에서는 정수형을 표현하는 방법 중, 음수 표현에 중점을 맞추었습니다.
MSB(최상위 부호 비트)를 사용하여 양수(0), 음수(1)를 나타내는 법과 문제점,
해결책으로 등장한 1’s complement(1의보수)표현법과
1의보수의 한계를 보완한 2’s complement(2의보수)표현법은
컴퓨터 프로그래밍에 있어 기초가 되는 내용이 아닐까 합니다.
물론, 더 자세한 연산 과정은

• ‘논리회로’
• ‘컴퓨터구조’(※추후 링크 업데이트 예정)
  와 같은 과목을 통해 더욱 자세히 알 수 있으니, 참고하시면 좋습니다.

이번에는 음수가 대략적으로 이렇게 표현이 된다는 부분까지만 설명하였습니다.

감사합니다.